Teoria de Markowitz (teoria da carteira) e a fronteira eficiente

A teoria de Markowitz, conhecida também como teoria da carteira ou teoria do portfólio, teve como grande diferencial apresentar o conceito de fronteira eficiente, demonstrando matematicamente os benefícios de ter uma carteira diversificada.

Quando o assunto é risco e retorno, podemos calcular o retorno de uma carteira de investimentos pela média ponderada dos retornos dos ativos.

Porém, a teoria do portfólio mostra que o risco de uma carteira não é dado simplesmente pela média do risco (medido pelo desvio-padrão) dos ativos individuais, pois é preciso considerar a correlação existente entre os ativos. Sendo assim, pode-se dizer que a “palavra-chave” que permeia a teoria de Markowitz é o conceito de diversificação, pois é este mecanismo que viabiliza reduzir o risco da carteira.

Siga a leitura deste artigo e entenda em detalhes a Teoria da Carteira de Harry Markowitz e os principais conceitos envolvidos, como a Carteira de Mínima Variância e a Fronteira Eficiente.

Quem é Harry Markowitz?

Harry Markowitz concluiu seu doutorado em economia pela Universidade de Chicago no ano de 1954, é autor de inúmeros livros e artigos científicos. Foi laureado, em 1990, com o prêmio Nobel de Economia, devido a sua contribuição na análise de risco e retorno de ativos financeiros.

Pode-se dizer que Harry Markowitz formalizou matematicamente a máxima de “não colocar todos os ovos em uma única cesta” para o contexto financeiro. Ele afirma que deve-se levar em conta a diversificação do risco na construção de portfólios, e que é possível construir uma série de portfólios, nos mais variados níveis de retorno exigidos, que sejam otimizados para a redução do risco.

A seguir serão mostrados mais detalhes a respeito de como a teoria de Markowitz trabalha cada um desses pontos: risco da carteira, minimização do risco, fronteira eficiente, etc.

A teoria de Markowitz (teoria da carteira)

Assaf Neto (2007) explica que a teoria de Markowitz faz parte do processo de avaliação de carteiras de investimentos, o qual envolve três grandes fases:

(i) a análise dos títulos, que trabalha com os fundamentos da avaliação de ativos, em que costuma-se encontrar o valor intrínseco de um título por descontar os fluxos futuros a uma taxa de atratividade;

(ii) a análise de carteiras, que envolve projeções de retorno esperado e do risco de um conjunto de ativos;

(iii) e a seleção de carteiras, que por sinal é o título do artigo de Markowitz (1952) – Portfolio Selection–, estuda a melhor combinação possível dos ativos analisados e sugere uma alocação de ativos dentro de uma carteira que maximize a satisfação do investidor. Na teoria de Markowitz essa satisfação é definida com base no que seria um “investidor racional”, que busca que seu risco seja mínimo para um dado nível de retorno.

Risco de uma carteira

Na época – em torno de 1952, quando o artigo “Portfolio selection” foi publicado – o risco de um ativo financeiro era medido pelo seu desvio-padrão. Ainda hoje, apesar de existirem diversas outras métricas, o desvio-padrão ainda é utilizado.

Nesse sentido, um dos principais pontos levantados na teoria de Markowitz é que o risco de um ativo medido isoladamente torna-se diferente quando esse ativo é incluído em uma carteira.

Em palavras do dia a dia, não se pode calcular o desvio-padrão de uma carteira simplesmente somando ou obtendo a média dos desvios de cada ativo isoladamente.

Isso ocorre porque há correlação entre as movimentações de diversos ativos financeiros. Para propor uma maneira de mensurar o risco de uma carteira foi que surgiu a teoria de Markowitz, a qual traz a equação do risco (desvio-padrão) de uma carteira de dois ativos (A e B) como sendo a seguinte:

   

Veja agora que se a carteira fosse composta por 3 ativos, a equação ficaria assim:

   

   

   

   

Sendo que é o risco, ou desvio-padrão da carteira; é o peso do ativo na carteira, ou seja, a participação percentual em relação ao total da carteira; é a variância de dado ativo e é a covariância do ativo A com o ativo B.

Diversificação: a grande vantagem de utilizar estes cálculos!

A teoria de Markowitz mostrou que na medida em que o investidor diversifica sua carteira, escolhendo ativos com correlação negativa, ele consegue reduzir, ou até eliminar (pelo menos na teoria) o risco diversificável (risco não sistemático).

A razão pela qual a diversificação melhora a relação risco e retorno é que, na medida em que novos ativos são adicionados a uma carteira de investimentos, o risco total, medido pelo desvio-padrão da carteira apresentado anteriormente, é reduzido. Já o retorno da carteira é determinado pela média ponderada dos retornos dos ativos individuais.

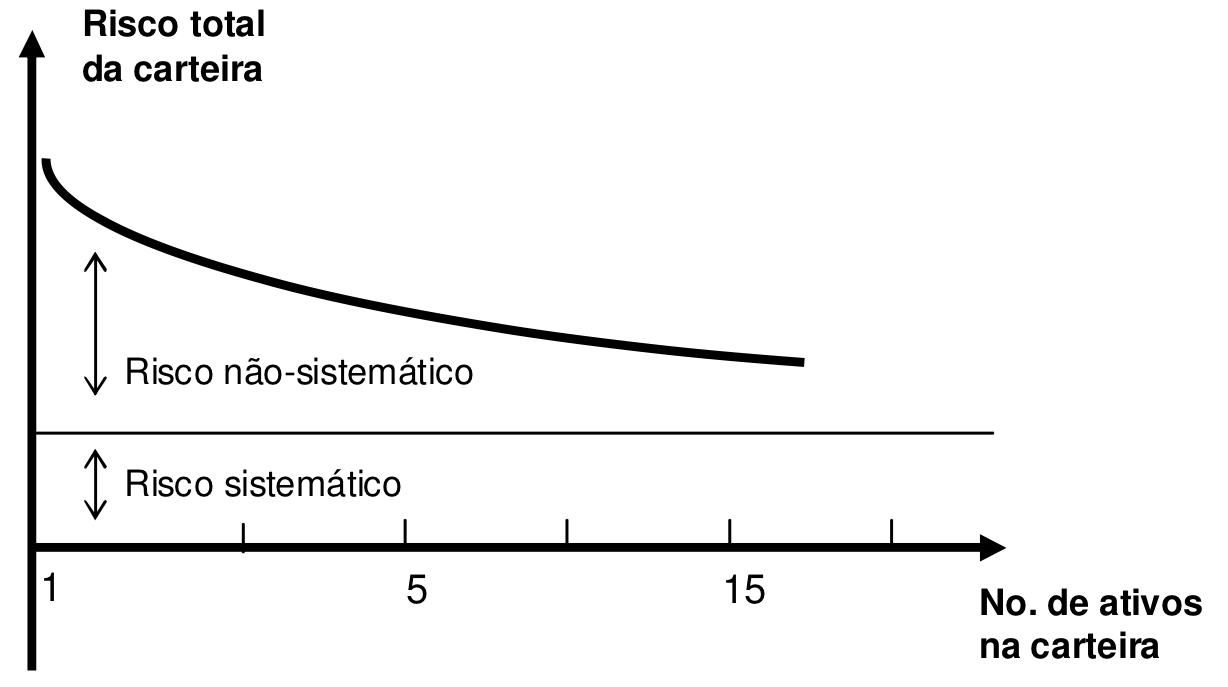
O risco diversificável (não sistemático) e risco não diversificável (sistemático)

O risco diversificável é aquele que pode ser eliminado por meio da diversificação da carteira.

Já o risco não diversificável é decorrente de questões sistêmicas. Como o nome fala, e refere-se a problemas macroeconômicos, desastres naturais, crise financeira, alta da inflação, entre outros.

A figura a seguir exemplifica bem como fica o risco da carteira em relação ao número de ativos que a compõem.

O princípio da dominância

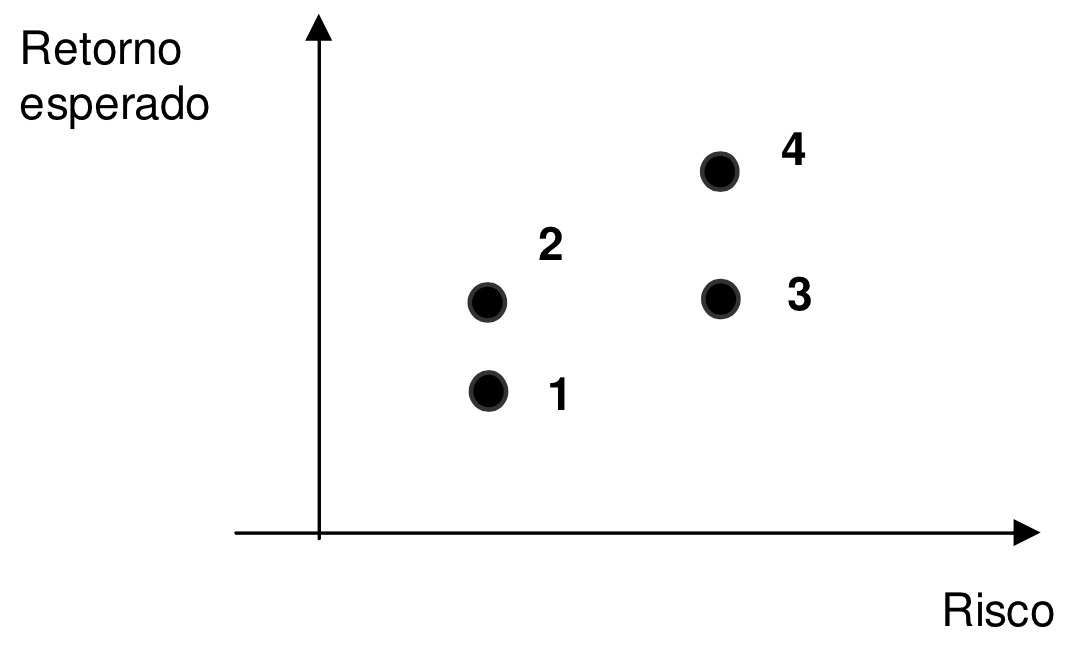
O princípio da dominância afirma que o investidor racional prefere o investimento que proporcione o maior retorno esperado para o mesmo nível de risco. Ou ainda o menor risco para o mesmo retorno esperado.

Observe a figura:

Com base nesse princípio, na figura acima é possível obter as seguintes conclusões:

• o ativo 2 domina o 1;
• o ativo 4 domina o 3;
• o ativo 2 domina o 3;

Contudo, nada pode-se dizer sobre o ativo 2 e o 4 e nem sobre o 1 e o 3! A escolha de um desses ativos dependerá do nível de aversão ao risco do investidor!

A carteira de mínima variância e a fronteira eficiente

Ao aplicarmos o princípio da dominância para todas as combinações possíveis de carteiras, chegamos a um dos pontos principais da teoria do portfolio de Markowitz: a “Carteira de Mínima Variância” (CMV).

O processo para encontrar a carteira de mínima variância (CMV) se resume em encontrar o portfólio ótimo através de um ponto de mínimo (derivada). Este portfólio será o de menor desvio-padrão dentre todas as combinações possiveis.

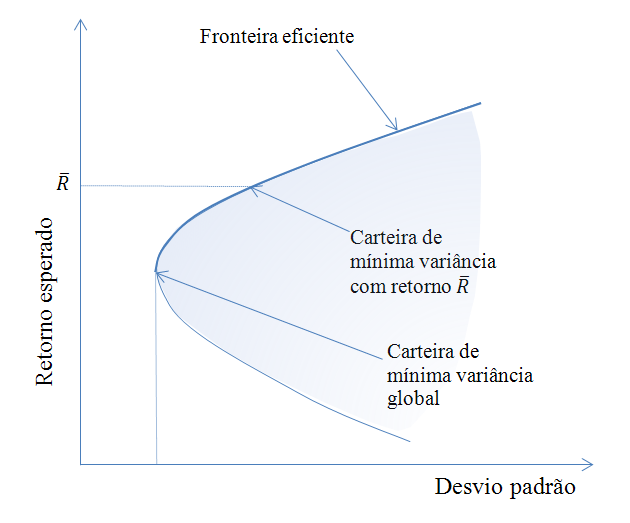
A partir da CMV, se fizermos um ponto em todas as combinações de ativos que possuem o menor nível de risco (desvio-padrão) para qualquer retorno superior ao da CMV, obteremos a “fronteira eficiente de Markowitz“.

Tanto a carteira de mínima variância, quanto a fronteira eficiente, são expressas no gráfico a seguir:

Conclusão

A teoria de Markowitz foi um marco histórico na literatura de finanças. O Capital Asset Pricing Model, entre outros modelos de apreçamento de ativos e diversas outras teorias emergiram baseadas nos pressupostos da teoria da carteira de Markowitz de que o investidor é racional e busca sempre reduzir o risco para um dado nível de retorno.

Posteriormente, com o advento das finanças comportamentais, percebeu-se que na verdade os investidores são sujeitos a heurísticas e vieses cognitivos que interferem o processo de tomada de decisão.

Para leitores mais interessados, Shefrin e Statman (2000), ícones das finanças comportamentais, desenvolveram a chamada “teoria comportamental da carteira”, que justamente traz aspectos psicológicos da tomada de decisão para um contexto de avaliação de ativos e análise de risco e retorno.

Referências

Assaf, N. A. (2007). Mercado financeiro. São Paulo: Editora Atlas.

Markowitz, H. (1952). Portfolio selection. The Journal of Finance, 7(1), 77–91.

Shefrin, H., & Statman, M. (2000). Behavioral portfolio theory. Journal of Financial and Quantitative Analysis, 35(2), 127–151. Ler.