Entre os modelos de aprendizado de máquina mais comuns e mais úteis estão as árvores de decisão. Elas são tão utilizadas porque fornecem ao usuário final uma fácil interpretação e desenham uma espécie de caminho a ser percorrido para alcançar um determinado objetivo. Entenda em detalhes neste artigo o que é árvore de decisão.
O que é árvore de decisão?
Uma árvore de decisão é uma ferramenta de suporte à tomada de decisão que usa um gráfico no formato de árvore e demonstra visualmente as condições e as probabilidades para se chegar a resultados. O algoritmo utilizado para chegar na representação visual da árvore pertence ao grupo de aprendizado de máquina supervisionado, e funciona tanto para regressão quanto para classificação.
Um árvore de decisão é uma forma de visualizar as regras de negócio que levam a determinados grupos de indivíduos, construídos com base em uma variável target. Por exemplo: “Quais são as regras, baseadas em variáveis pré-especificadas no modelo, que levam certos grupos de clientes a apresentarem uma menor taxa de churn, e outros uma taxa muito mais elevada?”
Em alguns casos de algortimos de machine learning, como redes neurais, por exemplo, os modelos podem acabar se tornando tão complexos que se tornam difíceis de serem explicados com facilidade. Já nos modelos de árvores de decisão os resultados são fáceis de explicar e de serem convertidos em decisões práticas de negócio no dia a dia das empresas.
Como funciona uma árvore de decisão?
O processo de construção do modelo da árvore se chama de indução, e pode exigir bastante poder computacional. O propósito da árvore de decisão é fazer diversas divisões dos dados em subconjuntos, de tal forma que os subconjuntos vão ficando cada vez mais puros. Um subconjunto dos dados será mais puro na medida em que contém menos classes (ou apenas uma) da variável target.
Uma forma de trabalhar matematicamente com a pureza é por meio da análise da entropia e do ganho de informação. Sendo assim, para entender como funciona o processo de construção de uma árvore de decisão é preciso compreender estes conceitos.
Entropia e ganho de informação
A decisão de dividir uma árvore recairá sobre a pureza em relação ao target, isso já vimos. A entropia é uma forma de medir a pureza de cada subconjunto de uma árvore de decisão.
Exemplificando, no caso de um conjunto de dados cuja variável target é binária (que indica a ocorrência ou não de um evento), a entropia é uma forma de medir a probabilidade de obter um elemento positivo (ocorrência do evento) a partir de uma seleção aleatória do subconjunto de dados.
Em outras palavras, podemos dizer quea entropia é uma medida de surpresa. A entropia vai de 0 a 1, e se ela for zero, então não há supresa nas respostas possíveis.
Outro conceito muito relacionado à entropia é o ganho informacional. O ganho de informação ocorre quando uma nova subdivisão dos dados provoca uma redução na entropia.
Entenda estes conceitos com um simples exemplo de jogar “cara ou coroa” com uma moeda.
Imagine, inicialmente, que uma moeda é totalmente viesada para cair sempre “cara”. O resultado será então compeltamente previsível, o que indica que não há ganho de informação na realizacão de um experimento como este. Ou seja, não há surpresas nos resultados possíveis.
Porém, se a moeda for um pouco menos viesada e vierem a cair mais de 50% de caras do que coroas, então há uma certa surpresa nos resultados, o que gera um ganho de informação.
Contudo, se toda vez que jogarmos a moeda cair apenas coroa, então voltamos a uma situação de zero entropia, em que não há surpresas.
Portanto, neste exemplo das moedas, a situação em que há maior entropia, ou maior nível de surpresa, ocorre quando a moeda é totalmente justa e o resultado do jogo de moedas não é previsível (apenas sabemos que os resultados possíveis recaem sobre cara ou coroa).
O ganho informacional é baseado na redução da entropia depois de uma divisão do conjunto de dados baseado em determinada regra. Construir uma árvore de decisão se trata de encontrar regras sobre as variáveis do modelo (ou pontos de corte) que retornam o maior ganho de informação, isto é, que tornam os ramos da árvore mais homogêneos, com menor entropia.
Ver explicações detalhadas sobre árvore de decisão. Caso tenha interesse, veja também este link, que contém explicações bastante claras e didáticas sobre entropia e ganho informacional.
Problemas de overfitting (sobreajuste) nas árvores de decisão
Uma árvore de decisão pode ficar bastante complexa, com uma elevada quantidade de arestas. Isso pode levar a um problema conhecido como overfitting, que se refere a uma resposta dada a uma situação extremamente específica no conjunto de dados de treino, a qual não será possível de ser generalizada.
Para resolver este tipo de situação existem métodos de “poda” (prune) das árvores de decisão. Na linguagem R é possível realizar a poda das árvores com o pacote rpart, usando a função prune().
Veja detalhes sobre poda de uma árvore de decisão no exemplo deste post sobre árvore de decisão aplicada ao contexto financeiro de avaliação de ações.
Como aplicar modelos de árvore de decisão no R?
Construir uma árvore de decisão no R é um procedimento simples. Existem diversos pacotes, mas um dos mais utilizados neste contexto é o rpart, que vamos usar aqui. Seguem alguns exemplos de árvore de decisão na linguagem R.
Exemplo 1. Árvore de decisão com R: dados do Titanic
Na sequência segue um exemplo de árvore de decisão utilizando um famoso conjunto de dados: Titanic. Veja como é o head dos dados:
# Pacotes a serem utilizados neste post
library(dplyr)
library(readr)
library(rpart)
library(rpart.plot)
library(xtable)
# Lendo os dados do titanic a partir de repositório, selecionando e tratando variáveis
titanic <- "https://gitlab.com/dados/open/raw/master/titanic.csv" %>%
read_csv %>%
select(survived, embarked, sex,
sibsp, parch, fare) %>%
mutate(
survived = as.factor(survived),
embarked = as.factor(embarked),
sex = as.factor(sex))
# Mostrando o head dos dados
print(xtable(head(titanic)), type = "html", digits = 2, include.rownames=FALSE)
| survived | embarked | sex | sibsp | parch | fare |
|---|---|---|---|---|---|
| 1 | S | female | 0 | 0 | 211.34 |
| 1 | S | male | 1 | 2 | 151.55 |
| 0 | S | female | 1 | 2 | 151.55 |
| 0 | S | male | 1 | 2 | 151.55 |
| 0 | S | female | 1 | 2 | 151.55 |
| 1 | S | male | 0 | 0 | 26.55 |
Nos dados, a nossa variável taget é survived, e indica se o indivíduo sobreviveu (=1), ou não (=0). As demais variáveis escolhidas indicam se o indivíduo embarcou (embarked), o gênero (sex), número de irmãos/cônjuges a bordo (sibsp = Number of Siblings/Spouses), número de pais/filhos a bordo (parch = Number of Parents/Children) e o valor da tarifa por passageiro (fare).
A árvore de decisão neste caso constrói as regras que definem os indivíduos que sobreviveram e os que não sobreviveram à tragédia ocorrida com o Titanic. Lembrando que a construção da árvore começa com a variável que maxima a pureza do conjunto de dados e mais minimiza a entropia.
Veja como fica a árvore de decisão para o Titanic:
# Separar os dados em treino e teste
set.seed(100)
.data <- c("training", "test") %>%
sample(nrow(titanic), replace = T) %>%
split(titanic, .)
# Criar a árvore de decisão
rtree_fit <- rpart(survived ~ .,
.data$training
)
rpart.plot(rtree_fit)
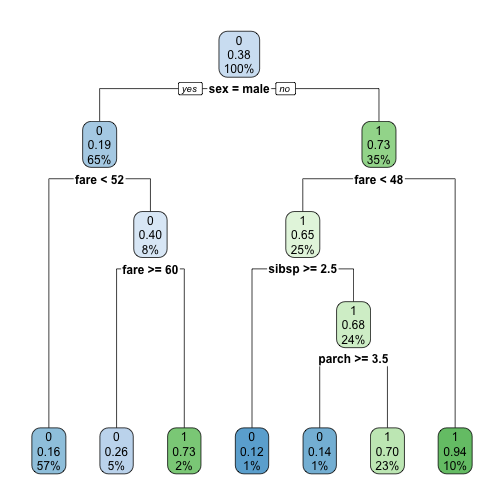
Vemos que a variável com menor entropia (a que gera a primeira divisão nos dados) é a variável de gênero. Na sequência vem a variável do preço da tarifa, que está diretamente correlacionada com o fato dos passageiros serem da primeira, segunda ou terceira classe. Neste ponto já conseguimos chegar na primeira regra: se o indivíduo era homem e havia pago menos de 52 na sua tarifa, então ele morreria. E este primeiro grupo (o primeiro grupo da esquerda) já corresponde a 56% do total de indivíduos.
O segundo grupo mais representativo é o penúltimo da esquerda para a direita, que corresponde à 23% do total de indivíduos no Titanic. Para chegar até este grupo, composto por 100% de sobreviventes, a regra da árvore de decisão ficou a seguinte: mulheres, que pagaram menos de 48 e tinham um bom número de familiares viajando também (mais de 2,5 entre irmãos e cônjuges, em média; e mais de 3,5 entre pais e filhos, em média). Por fim, se o indivíduo fosse mulher e houvesse pago mais de 48 na tarifa, então sobreviveria.
Este é um exemplo de como as árvores de decisão são intuitivas, pois constroem as regras que levam até grupos de alta e de baixa performance em relação à variável target.
Exemplo 2. Árvore de decisão com R: avaliação de ações de empresas
Este segundo exemplo é uma aplicação de árvore de decisão para o contexto financeiro. O propósito, para fins didáticos apenas, é identificar o perfil das melhores ações da B3, a bolsa brasileira, em termos de retorno histórico dos últimos 5 anos.
Veja como são as primeiras linhas dos dados (nem todas variáveis foram incluídas, pois são várias colunas):
# Lendo dataset de repositório
fundamentals <- "https://gitlab.com/dados/open/raw/master/br-stocks-fundamentals.csv" %>%
read_csv
# Selecionando algumas variáveis para mostrar o head
fundamentals %>%
arrange(desc(ret_anual)) %>%
select(codigo, ret_anual, pl, vm, p_vpa, divbr_pl) %>%
head() %>%
xtable() %>%
print(type = "html", digits = 2, include.rownames=FALSE)
| codigo | ret_anual | pl | vm | p_vpa | divbr_pl |
|---|---|---|---|---|---|
| MGLU3 | 90.31 | 35.93 | 14303781.95 | 7.53 | 34.30 |
| UNIP3 | 69.97 | 4.58 | 1823980.59 | 1.61 | 91.21 |
| REDE3 | 49.55 | 44.13 | 7713962.86 | 2.51 | 125.33 |
| BRKM3 | 43.98 | -11.18 | 34822965.99 | 7.26 | 473.09 |
| SUZB5+SUZB3 | 40.54 | 137.75 | 27983601.57 | 2.59 | 136.30 |
| RADL3 | 34.88 | 50.52 | 25124092.79 | 7.97 | 23.15 |
### Dicionário dos dados
# codigo: código da ação negociado em bolsa;
# ret_anual: retorno de 5 anos anualizado;
# pl: preço sobre lucro;
# vm: valor de mercado;
# p_vpa: preço sobre valor patrimonial;
# divbr_pl: dívida bruta sobre patrimônio líquido.
########
rtree2_fit <- rpart(ret_anual ~ .,
fundamentals %>% select(-codigo)
)
rpart.plot(rtree2_fit)
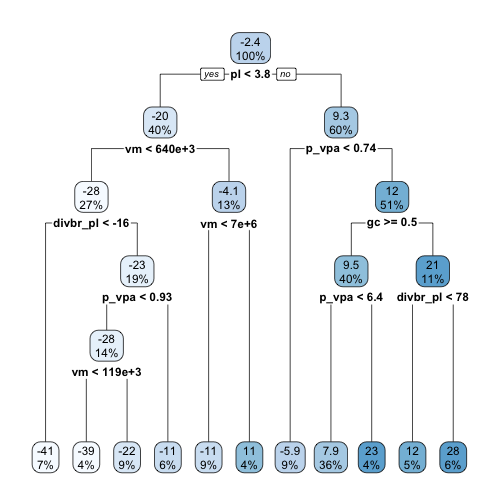
Aproveitando esta árvore como exemplo, é possível podar a árvore criada usando a função prune(), como comentado anteriormente. É preciso definir pelo menos o parâmetro cp a função, o qual representa um parâmetro de complexidade da árvore, sendo cp = 0 o caso mais complexo, e cp = 1 o caso menos complexo.
Existe uma forma de encontrar o CP ótimo para podar uma árvore de decisão pela linguagem R, como segue:
# Utilizar o valor de CP para o menor xerror da tabela
printcp(rtree2_fit)
## ## Regression tree: ## rpart(formula = ret_anual ~ ., data = fundamentals %>% select(-codigo)) ## ## Variables actually used in tree construction: ## [1] divbr_pl gc p_vpa pl vm ## ## Root node error: 111116/190 = 584.82 ## ## n=190 (171 observations deleted due to missingness) ## ## CP nsplit rel error xerror xstd ## 1 0.351814 0 1.00000 1.01265 0.131425 ## 2 0.084128 1 0.64819 0.78526 0.105784 ## 3 0.041562 2 0.56406 0.72771 0.097685 ## 4 0.031974 3 0.52250 0.66571 0.092172 ## 5 0.023387 4 0.49052 0.64700 0.085636 ## 6 0.019782 5 0.46713 0.64249 0.084772 ## 7 0.018929 6 0.44735 0.68382 0.085163 ## 8 0.014898 7 0.42842 0.68848 0.085718 ## 9 0.014535 8 0.41353 0.69174 0.085726 ## 10 0.011674 9 0.39899 0.69208 0.089450 ## 11 0.010000 10 0.38732 0.69481 0.089601
# Ver grraficamente o CP e o xerror
plotcp(rtree2_fit)
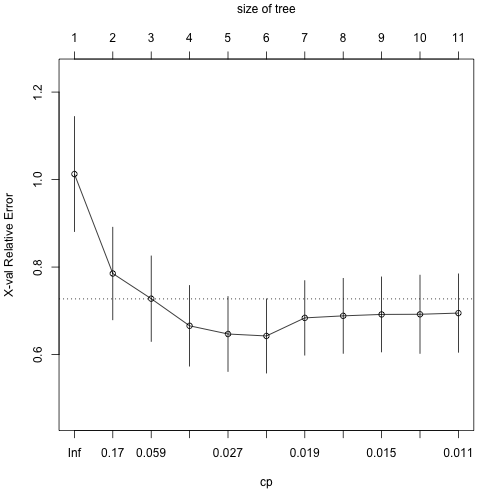
A árvore podada segue:
rpart.plot(prune(rtree2_fit, cp = 0.023387))
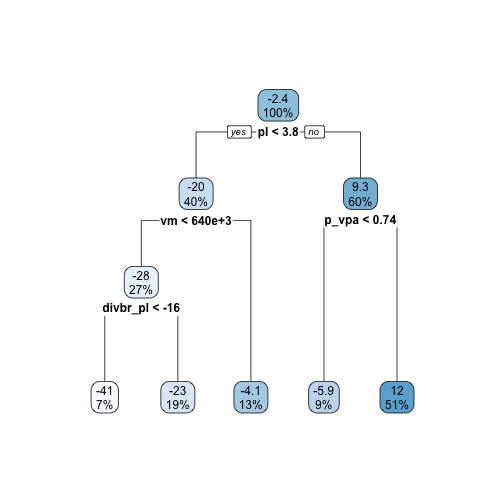
Veja como a poda da árvore de decisão foca apenas nas regras mais importantes. É muito importante realizar este passo para evitar overfitting, ou sobreajuste.
Mas e aí, o que a árvore de decisão pode nos trazer de conclusões neste dataset financeiro? O que a árvore fez neste caso foi desenhar o caminho que mostra como estão os indicadores fundamentalistas das empresas que mais geraram retorno na B3, a bolsa brasileira, nos últimos 5 anos.
Resumindo, se olharmos para um Preço/Lucro (pl) maior ou igual a 3,8; e ainda filtrarmos as ações com P/VPA (p_vpa) maior ou igual a 0,74, então chegaremos ao grupo com melhor rentabilidade anualizada dos últimos 5 anos. Este é o grupo mais da direita, composto por 140 ações que geram um retorno médio anual de 12%.
Que tal conferirmos nos dados se esta regra é verdadeira? A seguir utilizo filtros para chegar à lista do head das ações do melhor grupo, e na sequência a validação de que a média de retorno bate com o valor da árvore.
fundamentals %>%
filter(pl >= 3.8 & p_vpa >= 0.74) %>%
select(codigo, ret_anual, pl, vm, p_vpa, divbr_pl) %>%
arrange(desc(ret_anual)) %>%
head() %>%
xtable() %>%
print(type = "html",
digits = 2,
include.rownames = FALSE)
| codigo | ret_anual | pl | vm | p_vpa | divbr_pl |
|---|---|---|---|---|---|
| MGLU3 | 90.31 | 35.93 | 14303781.95 | 7.53 | 34.30 |
| UNIP3 | 69.97 | 4.58 | 1823980.59 | 1.61 | 91.21 |
| REDE3 | 49.55 | 44.13 | 7713962.86 | 2.51 | 125.33 |
| SUZB5+SUZB3 | 40.54 | 137.75 | 27983601.57 | 2.59 | 136.30 |
| RADL3 | 34.88 | 50.52 | 25124092.79 | 7.97 | 23.15 |
| ENGI3 | 34.01 | 30.81 | 9712213.34 | 3.30 | 216.64 |
Prova da média de retorno:
fundamentals %>%
filter(pl >= 3.8 & p_vpa >= 0.74) %>%
summarise(mean_return = mean(ret_anual, na.rm = TRUE))
## # A tibble: 1 x 1 ## mean_return ## <dbl> ## 1 12.0
Outros tipos de modelos de árvore de decisão
Random Forest
As Random Forests podem ser complicadas matematicamente, mas geralmente se referem a uma coleção de inúmeras diferentes árvores sendo questionadas a votarem em um resultado determinado.
Árvores de inferência condicional
Árvores de decisão são simples como condicionais do tipo “se isto, então aquilo”, as quais são relacionadas aos dados. Árvores de decisão de inferência condicional trabalham de forma semelhante, mas com algumas peculiaridades nos fundamentos estatísticos.
Conclusões: o que é árvore de decisão e como aplicar no R
Este artigo mostrou o que é árvore de decisão e como construir uma na linguagem R.
As árvores são simples, mas fornecem ótimos insights. Uma árvore de decisão é uma excelente ferramenta para auxiliar na definição de regras de negócio para se chegar a um determinado target. As árvores podem levar a overfitting, caso que pode ser resolvido com a poda da árvore de decisão.
Para realizar predições, métodos mais complexos e mais robustos, como as random forests são geralmente recomendados.
Referências
Introduction to Machine Learning with R: Rigorous Mathematical Analysis, O'Reilly Media. 2018. Ver.
Data Science for Business: What You Need to Know about Data Mining and Data-Analytic Thinking, O'Reilly Media. 2013. Ver.
Shannon entropy in the context of machine learning and AI. Ver