Derivativos: o que é o modelo Black and Scholes?

O desenvolvimento do modelo Black and Scholes permitiu uma formulação matemática para a precificação de opções, dentro do mercado de derivativos financeiros. O modelo foi elaborado por três economistas: Fischer Black, Myron Scholes e Bob Merton, por isso o modelo também é chamado de Black-Scholes-Merton. Entenda em detalhes neste artigo o que é o modelo Black and Scholes, o contexto em que é aplicado e detalhes sobre os apectos matemáticos que o envolvem.

Contextualização para o modelo Black-Scholes: o que são derivativos?

A instabilidade dos preços de diversos ativos gera incerteza na gerência de diversas instituições: governos, empresas, investidores, entre outros. Estas incertezas geram importantes e perigosos riscos operacionais. Neste contexto, alguns instrumentos de compartilhamento de riscos foram criados no mercado, com o objetivo de proteger as instituições das incertezas na dinâmica dos preços e garantir uma determinada posição para o futuro.

Podemos perceber diferentes tipos de usuários para o instrumento derivativo. Os hedgers, por exemplo, usam derivativos para reduzir os riscos que eles enfrentam de potenciais movimentos de uma variável de mercado, sendo conectados com os especuladores (aqueles que assumirão maiores riscos em busca de retornos futuros mais expressivos).

Um derivativo pode ser definido como um instrumento financeiro cujo valor depende de um ativo subjacente; este ativo pode ser uma ação, commodity, moeda, taxa de juros, índice, entre outras possibilidades. Porém, entre os derivativos financeiros, ainda existe uma ampla gama de classes diferentes: opções, futuros, swaps, etc…

Ao longo da história, o mercado de derivativos, que ajuda a unir especuladores e pessoas que buscam “travar” seus riscos (os hedgers), passou a se desenvolver cada vez mais. Tivemos avanços significativos a partir da segunda metade do século 19. O Chicago Board of Trade (CBOT), por exemplo, foi estabelecido em 1848 para unir fazendeiros e mercadores. Inicialmente, o principal objetivo era padronizar as quantidades e qualidades dos grãos que eram negociados. Já no século 20, um avanço significativo aconteceu quando o Chicago Board Options Exchange (CBOE) começou a negociar opções de ações em 1973.

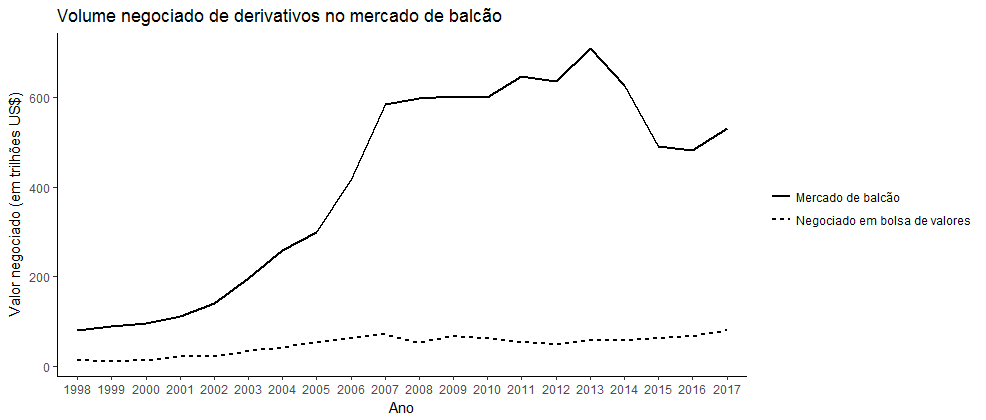
Porém, além dos mercados estruturados, muitas negociações se dão “over-the-counter” (OTC), que, em português é simplesmente chamado de mercado de balcão. Neste tipo de negociação, ao invés de uma única instituição que centraliza diversas negociações, como a própria CBOT já citada ou a Chicago Mercantile Exchange (CME), temos instituições financeiras, fundos de investimento e outras corporações como principais participantes dos mercados de balcão. Em 2015, o volume de negociações nas bolsas foi de US$80.98 trilhões, enquanto que no mercado de balcão foi de impressionantes US$531.91 trilhões, de acordo com o Bank for International Settlements (BIS), que regulamenta o mercado de derivativos pelo mundo. A figura a seguir demonstra estas afirmações.

O que é o modelo Black and Scholes?

Black and Scholes é um modelo simples e muito eficiente para determinar os preços teóricos de opções europeias (call e put) com base nos preços correntes de ações e outras variáveis. O modelo é muito difundido, porém, necessita que diversas premissas sejam satisfeitas (algumas até irreais na prática), o que levou à adptações da formulação original do modelo, como a inclusão dos efeitos de dividendos pagos durante a vida de uma opção.

Inicialmente, entenda o que significam os termos call e put e as diferenças entre opções europeias e americanas.

• Uma opção call lhe dá o direito de comprar o ativo subjacente (em geral uma ação negociada em bolsa de valores), enquanto que uma opção put lhe dá o direito de vendê-lo; tudo isto a partir de um determinado strike, que é o preço acordado pelas partes onde fica delimitado o direito de compra/venda.
• Já a diferença entre uma opção europeia e uma opção americana é o exercimento do direito: uma opção europeia só pode ser exercida na sua data de expiração, enquanto que a opção americana pode ser exercida a qualquer momento entre a data de início e a data de expiração.Então, como podemos precificar estes contratos? O modelo Black and Scholes possui importantes hipóteses na sua formulação. De acordo com Hull (2017), são as seguintes:
  • O preço do ativo subjacente (uma ação, uma moeda, etc…) é um processo estocástico;
  • A distribuição dos retornos do ativo subjacente é lognormal;
  • Os valores de retorno médio esperado e volatilidade são constantes;
  • Não há custos de transação;
  • Não há pagamento de dividendo durante a vida do derivativo;
  • Não existem condições de arbitragem, ou seja, obter retorno sem risco;
  • A taxa livre de risco “r” é constante.

Dinâmica dos preços do ativo subjacente no modelo Black and Scholes

“Qualquer variável cujo valor muda ao longo do tempo de forma incerta é dito que segue um processo estocástico” (Hull, 2017). Processos estocásticos podem ser descritos como discretos ou contínuos. Para a formulação do modelo, trataremos o processo na forma discreta, que é o que vemos na “vida real”.

Inspirado nos modelos físicos que tentam descrever a movimentação de partículas, Black e Scholes (1973) descreveram a dinâmica do preço do ativo subjacente como um movimento browniano, que é um processo estocástico. Algumas propriedades são de que as mudanças aleatórias são definidas por:

   

onde possui distribuição normal .

Por que a mudança no tempo é descrita com , e não somente ? Para variáveis aleatórias, como a definida em , cada mudança unitária em é independente, conforme traz Hull (2017):

“Qual é a distribuição de probabilidade de uma mudança no valor de uma variável aleatória durante dois anos? A mudança em dois anos é a soma de duas distribuições normais, cada uma com média igual a zero e variância igual a um. Por ser um processo estocástico do tipo Markov, as duas distribuições de probabilidades são independentes. Quando adicionamos duas distribuições normais independentes, o resultado é uma distribuição normal de probabilidades onde a média é igual a soma das média e a variância é igual a soma das variâncias.”

Desta forma, como o exemplo trazido, com uma distribuição de probabilidade representada por , ou seja, média zero e variância igual a dois, temos que o desvio padrão dessa distribuição de probabilidades é , já que o desvio padrão é a raiz da variância. Assim, o desvio padrão possui a dinâmica de . Assim, quanto maior for o período de tempo estudado para avaliar o valor da variável , maior será a incerteza inerente ao processo; também, maior será o seu desvio padrão, que é uma medida comum de incerteza no que se trata de dinâmica de preços.

Porém, além do componente aleatório z, o modelo Black & Scholes incorpora um componente determinístico em relação ao tempo. Assim, temos a seguinte descrição:

   

Assim, temos o que é chamado de processo generalizado de Wiener, ou, como já mencionado, movimento browniano. A equação (2) é melhor compreendida se analisarmos os componentes separadamente; como vimos, é a variável que adiciona ruído à variável , que a cada período de tempo , mudará b vezes. Já para o termo , temos que a mudança média esperada de , ou também chamada de drift rate, é a vezes por unidade de tempo. Assim, temos que o processo, em termos discretos, se dá por:

   

Porém, assumir que os coeficientes a e b são constantes não condizem com a realidade. O retorno médio esperado depende do valor de no momento , e o mesmo vale para a variabilidade, que também não será constante e mudará em função de . Assim, podemos descrever a equação diferencial discreta como:

   

Lema de Itô e sua aplicação à fórmula Black-Scholes

Porém, o que nos interessa não é entender a variação, mas sim, o processo como um todo. Ou seja, precisamos resolver esta equação diferencial estocástica. Entretanto, este problema não é trivial. Em Itô (1951), o autor conseguiu construir um teorema no qual se resolve uma equação diferencial estocástica, que hoje é chamado de “lema de Itô”. Assim, o lema de Itô nos mostra que uma equação diferencial do tipo pode ser resolvida da seguinte forma:

   

No entanto, é levarmos em conta que precisamos de uma medida em termos relativos, e não absolutos, para o desvio médio esperado. Assim, se temos que é o preço de uma ação no tempo , então o desvio médio esperado em será , sendo um percentual constante que indica o retorno esperado. Isso nos diz que um aumento esperado em será de , ou seja, (não levando em conta o fator aleatório).

Mas, como sabemos que existe aleatoriedade e incerteza no processo, é razoável assumirmos que a variabilidade dos retornos independe do preço do ativo subjacente. Como o mesmo afirma, “o investidor está incerto em relação aos retornos sendo o preço do ativo 10 ou 50” (Hull, 2017). Assim, o modelo Black & Scholes assume a volatilidade constante dos retornos do ativo subjacente pelo parâmetro . Desta forma, temos que o modelo ajustado da dinâmica de preços do ativo subjacente se dá por:

   

Assim, conforme construímos a equação (4) a partir do Lema de Ito, substituiremos os antigos coeficientes e pelas novas formulações e . Portanto, temos:

   

A hipótese de lognormalidade para à fórmula Black-Scholes

Se a distribuição dos retornos do ativo subjacente é lognormal, temos que avaliar o logarítmo dos preços do ativo subjacente. É definido, então, que , ONDE é o nosso processo originário da solução trazida pelo lema de Ito. Como:

   

então, temos que:

   

Então, vemos que a variação no preço do ativo subjacente segue um movimento browniano. O fator determinístico se dá por , enquanto que o fator de incerteza é representado pela variância constante . Uma variável possui uma distribuição lognormal se o logarítmo natural da respectiva variável é normalmente distribuída, que, a partir da equação anterior, pode ser comprovada por:

   

ou,

   

Derivação da equação diferencial de Black-Scholes-Merton

A partir do método de valoração neutra ao risco, é possível chegar na equação diferencial de Black-Scholes-Merton:

   

Esta solução busca eliminar a possibilidade e arbitragem, usando as derivações obtidas a partir da solução do lema de Itô.
A solução desta equação diferencial pode ser realizada por alguns métodos diferentes, mas que não fazem parte do escopo deste post. Entretanto, o objetivo é chegar nas formulas de precificação que tornam possível mensurar o valor presente de uma opção put e call, que são as seguintes:

   

para uma call, e para uma put:

   

onde:

   

sendo:
– a função cumulativa da distribuição de probabilidade para uma distribuição normal;
– o preço do ativo subjacente hoje;
– o valor do strike da opção
– sendo a taxa livre de risco (a SELIC, por exemplo);
– o intervalo de tempo para a expiração da opção, em anos;
– E como a volatilidade anual esperada para o ativo subjacente.

Considerações sobre o modelo Black and Scholes

O modelo Black & Scholes é amplamente utilizado na indústria financeira e, inclusive, garantiu o prêmio Nobel de Economia em 1997 aos seus pesquisadores, por sedimentar um campo de pesquisa na área de riscos e mensuração de derivativos, o que, como percebemos, envolve uma matemática avançada.

Hoje, os modelos avançaram muito, quebrando algumas das pesadas hipóteses que os pesquisadores assumiram; a hipótese de volatilidade constante, por exemplo, é uma das mais discutidas, muito por conta da existência dos “smiles de volatilidade”. Contudo, o modelo Black and Scholes é considerado o “feijão com arroz”, já que é amplamente utilizado e possui uma forma analítica mais fácil de ser compreendida do que outros modelos estudados na academia.

Referências

Black, Myron, Fischer e Scholes. 1973. “The Pricing of Options and Corporate Liabilities.” Journal of Political Economy 81 (3). The University of Chicago Press: 637–54.

Hull. 2017. Options, Futures and Other Derivatives/John c. Hull. Upper Saddle River, NJ: Prentice Hall,

Itô, Kiyosi. 1951. On Stochastic Differential Equations. Vol. 4. American Mathematical Soc.

---

Autor convidado: Gabriel Dias

Estudante de economia da Universidade do Estado de Santa Catarina. Possui experiência na solução de problemas de negócio a partir de modelagem estatística/matemática, automatizando tomadas de decisão.
LinkedIn.