A Análise de Componentes Principais (ACP), ou Principal Component Analysis (PCA), é uma técnica de ciência de dados que viabiliza reduzir grande parte das variáveis de um conjunto de dados em poucos componentes principais que explicam grande parte da variação dos dados.
Em que contexto o PCA é útil?
Podemos comparar duas variáveis (colunas em uma tabela de dados) de cada vez se usarmos diagramas de dispersão (scatter plots). Porém, veja a quantidade necessária de scatter plots dependendo da quantidade de variáveis a serem comparadas:
- 2 variáveis (A,B) = 1 scatter = (AxB)
- 3 variáveis (A,B,C) = 3 scatters = (AxB), (AxC), (BxC)
- 4 variáveis (A,B,C,D) = 6 scatters = (AxB), (AxC), (AxD), (BxC), (BxD), (CxD)
Imagine agora um conjunto de dados com dezenas ou centenas de variáveis:
Além da enorme quantidade de scatter plots necessários, fica extremamente inviável conseguir analisar todos esses gráficos e tirar valor deles com análises visuais.
Neste contexto, o uso da Análise de Componentes Principais se torna útil.
O que é PCA (Análise de Componentes Principais)?
O PCA é uma técnica estatística de ciência de dados capaz de resumir as variáveis de um conjunto de dados em “componentes principais” que contém a maior parte da variância das variáveis originais. O PCA recria os dados de uma forma mais representativa por meio de combinações lineares das variáveis.
A quantidade (n) de componentes principais será igual ao número de variáveis originais. Contudo, normalmente em poucos componentes praticamente toda correlação das variáveis originais é “absorvida” e 2 ou 3 componentes contemplam praticamente toda a variância do conjunto de dados.
Os componentes principais (PC's) são classificados por ordem de explicação da variância. Sendo assim, o PC1 explica mais a variabilidade dos dados do que o PC2, e assim por diante.
Como apresentar os resultados de um PCA?
Um procedimento que costuma-se fazer para visualizar melhor o impacto das variáveis com o auxílio do PCA (Análise de Componentes Principais) é utilizar gráficos de dispersão (scatter plot) entre 2 componentes principais (PC's) de cada vez.
Além disso, também é possível mostrar a direção para a qual cada variável original aponta no espaço 2D de cada scatter plot. Este tipo de gráfico é chamado de biplot.
Casos de uso da Análise de Componentes Principais
Dois dos principais casos de uso do PCA são:
- Análise exploratória, como identificar visualmente no biplots como as variáveis se relacionam dentro dos componentes.
- Redução de dimensionalidade: reduz o tempo de processamento e pode melhorar os resultados de modelos preditivos ao usar PCA nos dados de treino e teste.
Existem ainda casos de uso do PCA que são mais específicos, como compressão de imagens, por exemplo.
Como funciona o PCA?
Partimos de um conjunto de dados (dataset) com as variáveis originais e chegamos a um dataset reduzido a “compontes principais”.
- A grosso modo, procura encontrar “linhas retas” que melhor expressam as direções dos dados em multi-dimensões.
- Não é recomendado para variáveis categóricas (apenas numéricas).
- Se concentra nas direções que definem a maior parte da variância dos dados.
- Autovetor (eigenvector): é a direção (vertical ou 45 graus).
- Autovalor (eigenvalue): é um número que expressa o quanto há de variância naquela direção.
O autovetor com maior autovalor é o primeiro componente principal.
Aplicando PCA no conjunto de dados mtcars na linguagem R
O conjunto de dados “Motor Trend Car Road Tests” foi extraído de uma revista automobilística de 1974 e contempla 10 variáveis que representam características ou métricas de desempenho dos veículos. Os dados são nativos da distribuiçã básica da linguagem R, basta digitar mtcars no console do RStudio. Para informações, como dicionário de dados, basta digitar ? mtcars, e accessar a documentação de ajuda.
Veja o head dos dados:
data <- mtcars %>% dplyr::select(-c("vs", "am"))
print(
xtable(data %>% head(5)),
type = "html"
)
| mpg | cyl | disp | hp | drat | wt | qsec | gear | carb | |
|---|---|---|---|---|---|---|---|---|---|
| Mazda RX4 | 21 | 6 | 160 | 110 | 3.90 | 2.62 | 16.46 | 4 | 4 |
| Mazda RX4 Wag | 21 | 6 | 160 | 110 | 3.90 | 2.88 | 17.02 | 4 | 4 |
| Datsun 710 | 22.80 | 4 | 108 | 93 | 3.85 | 2.32 | 18.61 | 4 | 1 |
| Hornet 4 Drive | 21.40 | 6 | 258 | 110 | 3.08 | 3.21 | 19.44 | 3 | 1 |
| Hornet Sportabout | 18.70 | 8 | 360 | 175 | 3.15 | 3.44 | 17.02 | 3 | 2 |
Basta então aplicar a função prcomp, nativa do R Stats, a qual executa a Análise dos Componentes Principais (PCA).
mtcars.pca <- prcomp(data, center = TRUE, scale. = TRUE)
Cada análise de PCA resulta em um número de componentes principais igual ao número de variáveis. Porém, não pode-se dizer que um PCA é análogo a uma determinada variável.
Inclusive, um dos pontos negativos do PCA é que os números resultantes dos Componentes Principais não possuem uma interpretação plausível, como é possível interpretar os próprios valores das variáveis originais, por exemplo.
A seguir, é apresentado resumo da importância de cada um dos componentes principais identificados no exemplo acima na linguagem R. Obs.: Nem todos componentes são apresentados para a tabela ficar visível na tela, mas no total seriam 9 Componentes Principais (mesmo número de variáveis).
summary(mtcars.pca)$importance
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | |
|---|---|---|---|---|---|---|
| Standard deviation | 2.38 | 1.44 | 0.71 | 0.51 | 0.43 | 0.35 |
| Proportion of Variance | 0.63 | 0.23 | 0.06 | 0.03 | 0.02 | 0.01 |
| Cumulative Proportion | 0.63 | 0.86 | 0.92 | 0.95 | 0.97 | 0.98 |
Veja que os 4 primeiros componentes principais já são responsáveis por 95% da porporção da variância dos dados (linha Cumulative Proportion.
Segue o head dos 4 primeiros componentes principais, em que cada linha é uma linha de dado (um carro) e cada coluna é substituída por um componente principal (que não mais representa nenhuma coluna especificamente, mas contém variância “misturada” das variáveis originais):
mtcars.pca$x[,1:4] %>% head(10)
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| Mazda RX4 | -0.66 | 1.17 | -0.20 | -0.13 |
| Mazda RX4 Wag | -0.64 | 0.98 | 0.11 | -0.09 |
| Datsun 710 | -2.30 | -0.33 | -0.21 | -0.11 |
| Hornet 4 Drive | -0.22 | -1.98 | -0.33 | -0.31 |
| Hornet Sportabout | 1.59 | -0.83 | -1.03 | 0.15 |
| Valiant | 0.05 | -2.45 | 0.11 | -0.87 |
| Duster 360 | 2.71 | 0.36 | -0.65 | 0.10 |
| Merc 240D | -2.04 | -0.80 | 0.85 | -0.27 |
| Merc 230 | -2.30 | -1.31 | 1.97 | 0.05 |
| Merc 280 | -0.38 | 0.58 | 0.89 | 0.07 |
Visualizando graficamente os resultados do PCA
É possível também criar um biplot para visualizar como cada variável impacta nas relações entre os componentes principais. Para isso vamos usar o pacote de visualização highcharter.
Agora, veja o gráfico biplot que compara o PC1 e PC2 e mostra como cada variável impactou na construção de cada componente. Cada ponto do gráfico corresponde a uma linha de dado (dataset com 32 linhas no total).
# Criando Biplot para PC1 e PC2
highcharter::hchart(mtcars.pca, choices = 1:2) %>%
highcharter::hc_title(text = "Biplot para PC1 e PC2") %>%
highcharter::hc_xAxis(title = list(text = "PC1")) %>%
highcharter::hc_yAxis(title = list(text = "PC2"))
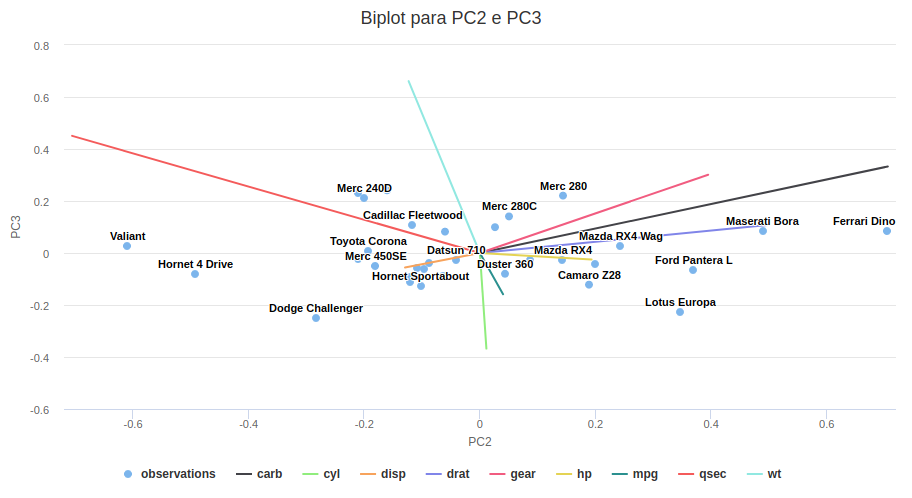
Por fim, segue gráfico biplot comparando PC2 e PC3.
# Criando Biplot para PC2 e PC3
highcharter::hchart(mtcars.pca, choices = 2:3) %>%
highcharter::hc_title(text = "Biplot para PC2 e PC3") %>%
highcharter::hc_xAxis(title = list(text = "PC2")) %>%
highcharter::hc_yAxis(title = list(text = "PC3"))
Considerações sobre a Análise de Componentes Principais
O resultado de uma análise de componentes principais pode ser utilizado para estimar outros modelos.
Veja, se você possui um dataset com um número muito grande de variáveis, o PCA viabiliza que haja uma redução de muitas variáveis para poucos componentes principais que expressem a maior parte da variância dos dados.
A maior dificuldade do uso do PCA, contudo, é analisar os resultados depois, pois não há uma interpretação “real” para os valores dos componentes principais.