No CAPM o risco sistemático é representado pelo coeficiente $beta$. No contexto corporativo o CAPM pode ser utilizado para calcular o custo de capital próprio, através da reta característica.
begin{equation}
E(R_i) = R_f + beta_{im}[E(R_m) – R_f],
label{eq:capm}
end{equation}
sendo que:
- $E(R_i)~~$ representa o retorno esperado de um certo ativo ou portfólio. Significa que o retorno esperado de um ativo será a taxa livre de risco ($R_f~$) mais o prêmio por unidade de risco $[E(R_m) – R_f]$, medido pelo $beta$.
- $R_f~$ é a taxa de juros livre de risco
- $beta_{im}~~$ é o coeficiente beta, que representa a sensibilidade dos retornos do ativo em relação aos do mercado, ou também:
begin{equation}
beta_{im} = frac {mathrm{Cov}(R_i,R_m)}{mathrm{Var}(R_m)},
label{eq:beta}
end{equation} - $E(R_m)~$ é o retorno esperado do mercado
- $E(R_m)-R_f~$ é por vezes chamado de ”prêmio de mercado” ou ”prêmio de risco”, e representa a diferença entre a taxa de retorno esperada do mercado e a taxa de retorno livre de riscos.
temporal utilizando o CAPM. Esta regressão incluiu o chamado “alfa de Jensen”,
representado pelo termo de intercepto, ou seja, a constante do modelo de
regressão linear simples. Esta constante, apesar de sua simplicidade,
desempenha um importante papel na comparação de opções de investimentos, pois é
o alfa que mede o retorno anormal de um ativo ou carteira em relação ao seu benchmark. Sendo assim, o CAPM no
formato de regressão de série temporal pode ser expresso por:
begin{equation}
(R_{i,t} – R{f,t}) = alpha + beta(R_{m,t} – R_{f,t}) + epsilon_t .,
label{eq:capm_jensen}
end{equation}
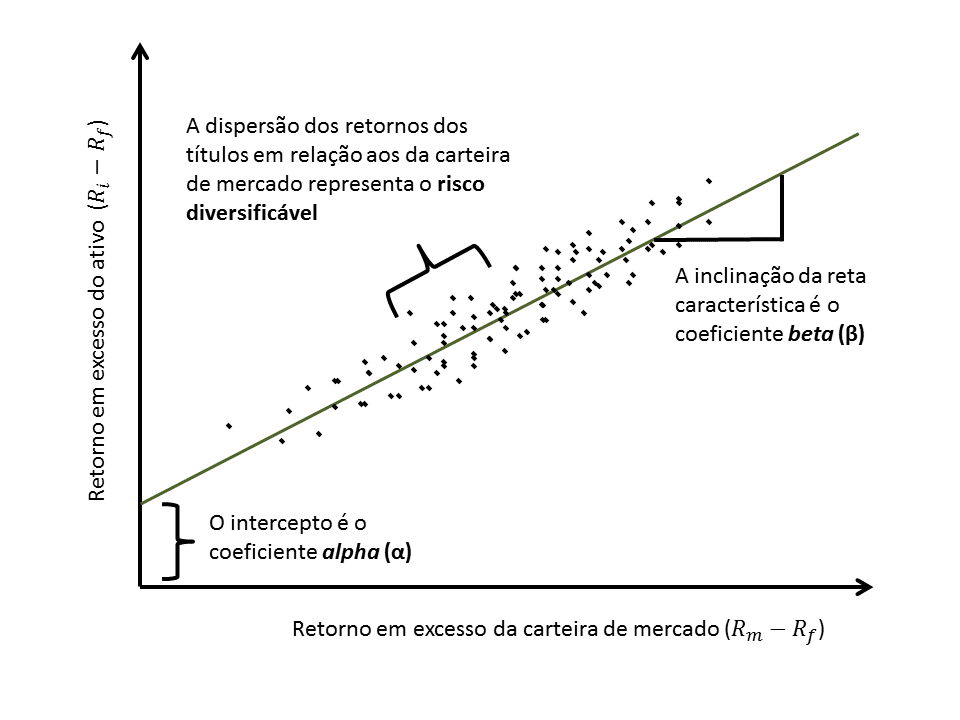
A Equação ref{eq:capm_jensen} é conhecida como a reta característica e é demonstrada pela figura abaixo:
O intercepto da regressão linear, denominado de alpha para este contexto, indica o retorno em excesso – ou anormal – para o caso de assumirmos que a carteira de mercado não possui excesso de retorno. A figura acima serve mais para fins didáticos, mas na prática o alpha poderá ser negativo ou nulo. Além disso, por estarmos falando de renda variável, dificilmente os pontos do gráfico de dispersão ficarão apenas no campo positivo.
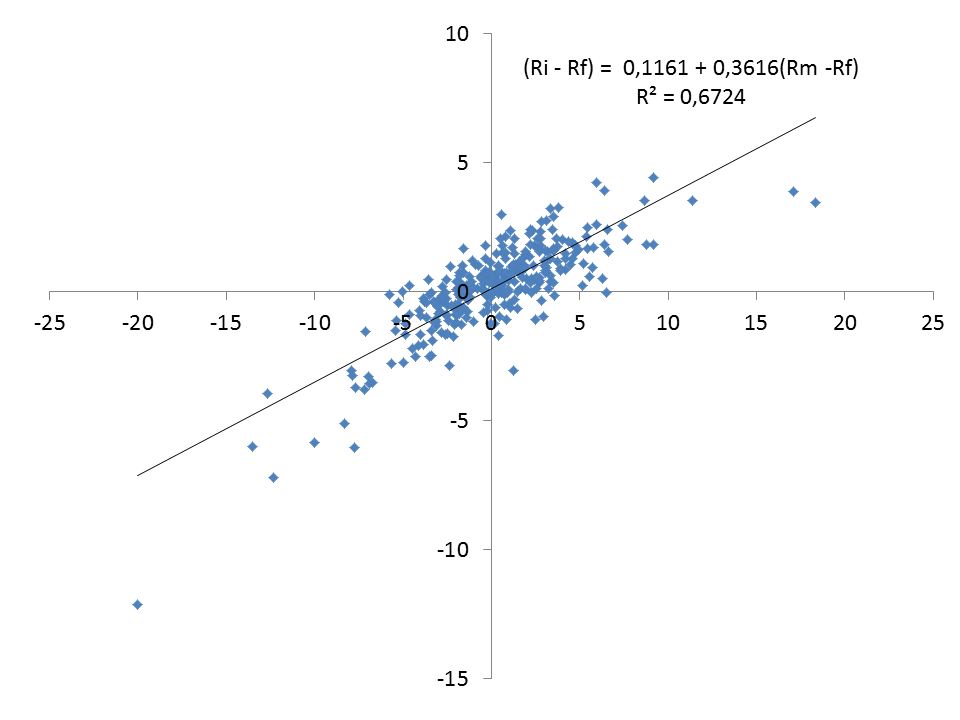
A próxima figura demonstra uma situação real da reta característica, na qual o eixo X é representado pelos retornos do Ibovespa e o eixo Y pelos retornos de uma carteira composta por ativos de médio de valor de mercado durante o período de janeiro de 2007 até dezembro de 2013. A periodicidade dos dados é semanal e a taxa livre de risco utilizada neste exemplo foi o CDI:
Premissas do modelo CAPM
- Os investidores são racionais e procuram maximizar sua utilidade econômica. Cada indivíduo se preocupa apenas com o retorno esperado e o risco de um determinado ativo;
- Os investidores existem em grande número e se comportam de forma competitiva. Um único investidor não pode provocar variações nos preços;
- O horizonte de tempo considerado nas expectativas de todos os investidores é o mesmo;
- Todos os investidores possuem o mesmo nível de acesso a todos os ativos;
- Não existem taxas, corretagens ou outros custos de transação;
- Todos os investidores possuem as mesmas crenças sobre as oportunidades de investimento, ou seja, possuem expectativas homogêneas;
- Os investidores podem emprestar e tomar emprestado montantes ilimitados de recursos à taxa livre de risco;
- Os investidores podem vender a descoberto qualquer ativo, bem como reter qualquer fração de uma determinada ação.
Características do beta
| Beta | Risco | Ativo | O que ocorre |
| 0 | Não há | Livre de risco | Quando o beta é zero significa que o retorno esperado será igual ao ativo livre de risco |
| Menor que 1 |
Baixo | Defensivo | O ativo gera retorno abaixo do mercado, mas é menos arriscado |
| Igual a 1 | Médio | Mercado | O retorno é igual ao retorno do mercado |
| Maior que 1 |
Alto | Agressivo | O ativo gera retorno acima do mercado e é mais arriscado |
Considerações
O CAPM é um modelo que permite estimar o retorno esperado de um ativo em relação a uma dada carteira de mercado perfeitamente diversificada. Através do coeficiente “beta” o CAPM consegue captar o risco sistemático (ou não diversificável), ou seja, o risco que não pôde ser diversificado na carteira de mercado.
O CAPM faz parte do conjunto teórico das finanças denominado de “finanças tradicionais” e tem como uma de suas desvantagens a quantidade de premissas que devem ser assumidas para que o modelo se torne confiável.
Questões de concursos
a) o risco diversificável do ativo.
b) o risco de crédito do ativo.
c) o coeficiente de correlação do ativo com o mercado.
d) o risco de liquidez do ativo.
e) o risco não diversificável do ativo.
Clique aqui e veja o gabarito
Letra E. O beta representa o risco sistemático ou não diversificável. É muito importante gravar estes sinônimos: risco diversificável = risco não sistemático; risco não diversificável = risco sistemático. Enquanto o risco sistemático é representado pelo beta, o não sistemático é representado pela dispersão dos retornos dos títulos em relação aos movimentos do retorno da carteira de mercado.
Logo, o custo esperado de capital próprio de X, em % ao ano, é:
a) menor que 8%
b) igual a 8%
c) igual a 10%
d) maior que 8% e menor que 10%
e) maior que 10%
Clique aqui e veja o gabarito
Letra E. Para resolver esta questão basta substituir os valores pela equação do CAPM (Equação ref{eq:capm}). O enunciado nos dá quase todas as variáveis necessárias para encontrarmos o retorno esperado, que neste contexto está sendo tratado como o custo de capital próprio da companhia. A única variável que está faltando é o beta. No entanto, o enunciado afirma que a ação ordinária da companhia é um ativo agressivo, logo o seu beta deverá ser maior que 1. Se substituirmos os valores pela equação do CAPM teremos que:
k = Rf + beta x (Rm – Rf)
k = 8 + 1 x (10 – 8)
k = 10%
Neste caso “k” representa o custo de capital. Sendo que o beta deverá ser maior que 1, logo podemos afirmar que k será maior que 10%.